If a group might come against a non-group the match wouldn't be fair nor fun... I hope that would be impossible with the system your suggesting
A group could only go against a group both already pre prepared
- Medi3vil likes this
![]() Posted by Susej
on 11 November 2014 - 13:38
Posted by Susej
on 11 November 2014 - 13:38
Yep that would be awesome i cant remmeber the number of times i have asked in chat what server i am.

![]() Posted by Susej
on 07 November 2014 - 11:43
Posted by Susej
on 07 November 2014 - 11:43
This is small issue but frustrating.
Can we please get gem order sorted out. Lots of people know about the ambers being weird (fair and glilm sort the wrong way around).
But as you can see in this picture
Radiant rubies are not even grouped with rubies...
MY OCD IS TINGLING
![]() Posted by Susej
on 20 July 2014 - 17:09
Posted by Susej
on 20 July 2014 - 17:09
But give a separate complete set bonus to favor pures as well. But not a stat set bonus, something else more interesting, say a buff to the ultimate spell in talent tree -> full mage fabled -> +4 sec to DB, or something.
Actually more time would only be good on dungeons i would like db to hit 250% dps and a wider aoe
to prophet when snowfall is on to add attack power to team members
to warrior frenzy to give + haste or so
to ranger to increase bow attacking speed( to match xbow)
to sin to make make shock treatment more powerfull
tank to give phallanx a reflect damage of 25% or no repairs during that timeor something like that
![]() Posted by Susej
on 12 July 2014 - 16:37
Posted by Susej
on 12 July 2014 - 16:37
Prophets with repent and level 50 "sorcery sword and shield" are gonna be OP
Along with glaciate a team member when he is about to die and heal him back to full health while prophet goes repent/reju/redepmtion/rigtheus defense/ and if needed why not 4 second despair at a whole area and radiance.
i am gonna love when that happens, and i will be doing pvp by then
still 8.5 secs silence with a lovelly bleed selection will wipe it out if fast enough(if not attentive and fast enough to cast repent)
ranger will have tornado and at that speed and distance its gonna be hard to survive that crystal blast-tornado-blood fang-creeping vines...
but still repent with shield and sorcery blade sounds like paradise for me
![]() Posted by Susej
on 11 July 2014 - 09:50
Posted by Susej
on 11 July 2014 - 09:50
![]() Posted by Susej
on 11 July 2014 - 08:44
Posted by Susej
on 11 July 2014 - 08:44
![]() Posted by Susej
on 29 June 2014 - 12:12
Posted by Susej
on 29 June 2014 - 12:12
lol
Let me help you zeus
The scientific study of probability is a modern development. Gambling shows that there has been an interest in quantifying the ideas of probability for millennia, but exact mathematical descriptions arose much later. There are reasons of course, for the slow development of the mathematics of probability. Whereas games of chance provided the impetus for the mathematical study of probability, fundamental issues are still obscured by the superstitions of gamblers.[10]
According to Richard Jeffrey, "Before the middle of the seventeenth century, the term 'probable' (Latin probabilis) meant approvable, and was applied in that sense, univocally, to opinion and to action. A probable action or opinion was one such as sensible people would undertake or hold, in the circumstances."[11] However, in legal contexts especially, 'probable' could also apply to propositions for which there was good evidence.[12]
Aside from elementary work by Gerolamo Cardano in the 16th century, the doctrine of probabilities dates to the correspondence of Pierre de Fermat and Blaise Pascal (1654). Christiaan Huygens (1657) gave the earliest known scientific treatment of the subject.[13]Jakob Bernoulli's Ars Conjectandi (posthumous, 1713) and Abraham de Moivre's Doctrine of Chances (1718) treated the subject as a branch of mathematics.[14] See Ian Hacking's The Emergence of Probability[9] and James Franklin's The Science of Conjecture[full citation needed] for histories of the early development of the very concept of mathematical probability.
The theory of errors may be traced back to Roger Cotes's Opera Miscellanea (posthumous, 1722), but a memoir prepared by Thomas Simpson in 1755 (printed 1756) first applied the theory to the discussion of errors of observation.[citation needed] The reprint (1757) of this memoir lays down the axioms that positive and negative errors are equally probable, and that certain assignable limits define the range of all errors. Simpson also discusses continuous errors and describes a probability curve.
The first two laws of error that were proposed both originated with Pierre-Simon Laplace. The first law was published in 1774 and stated that the frequency of an error could be expressed as an exponential function of the numerical magnitude of the error, disregarding sign. The second law of error was proposed in 1778 by Laplace and stated that the frequency of the error is an exponential function of the square of the error.[15] The second law of error is called the normal distribution or the Gauss law. "It is difficult historically to attribute that law to Gauss, who in spite of his well-known precocity had probably not made this discovery before he was two years old."[15]
Daniel Bernoulli (1778) introduced the principle of the maximum product of the probabilities of a system of concurrent errors.
Adrien-Marie Legendre (1805) developed the method of least squares, and introduced it in his Nouvelles méthodes pour la détermination des orbites des comètes (New Methods for Determining the Orbits of Comets).[citation needed] In ignorance of Legendre's contribution, an Irish-American writer, Robert Adrain, editor of "The Analyst" (1808), first deduced the law of facility of error,
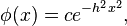
where  is a constant depending on precision of observation, and
is a constant depending on precision of observation, and  is a scale factor ensuring that the area under the curve equals 1. He gave two proofs, the second being essentially the same as John Herschel's (1850).[citation needed]Gauss gave the first proof that seems to have been known in Europe (the third after Adrain's) in 1809. Further proofs were given by Laplace (1810, 1812), Gauss (1823), James Ivory (1825, 1826), Hagen (1837), Friedrich Bessel (1838), W. F. Donkin (1844, 1856), and Morgan Crofton (1870). Other contributors were Ellis (1844), De Morgan (1864), Glaisher (1872), and Giovanni Schiaparelli (1875). Peters's (1856) formula[clarification needed] for r, the probable error of a single observation, is well known.[to whom?]
is a scale factor ensuring that the area under the curve equals 1. He gave two proofs, the second being essentially the same as John Herschel's (1850).[citation needed]Gauss gave the first proof that seems to have been known in Europe (the third after Adrain's) in 1809. Further proofs were given by Laplace (1810, 1812), Gauss (1823), James Ivory (1825, 1826), Hagen (1837), Friedrich Bessel (1838), W. F. Donkin (1844, 1856), and Morgan Crofton (1870). Other contributors were Ellis (1844), De Morgan (1864), Glaisher (1872), and Giovanni Schiaparelli (1875). Peters's (1856) formula[clarification needed] for r, the probable error of a single observation, is well known.[to whom?]
In the nineteenth century authors on the general theory included Laplace, Sylvestre Lacroix (1816), Littrow (1833), Adolphe Quetelet (1853), Richard Dedekind (1860), Helmert (1872), Hermann Laurent (1873), Liagre, Didion, and Karl Pearson. Augustus De Morgan and George Boole improved the exposition of the theory.
Andrey Markov introduced[citation needed] the notion of Markov chains (1906), which played an important role in stochastic processes theory and its applications. The modern theory of probability based on the measure theory was developed by Andrey Kolmogorov (1931).[citation needed]
On the geometric side (see integral geometry) contributors to The Educational Times were influential (Miller, Crofton, McColl, Wolstenholme, Watson, and Artemas Martin).[citation needed]
MOBILE SITE | TERMS OF USE | PRIVACY POLICY | COOKIE POLICY | REPORT SPAM | PRESS | CONTACT US
©2013 HUNTED COW STUDIOS. ALL RIGHTS RESERVED Find content
Find content